Today Alex Kavvos, a DPhil candidate in Computer Science at the University Oxford, and College Lecturer at University College, Oxford, tells us about mathematical theories and their links to computer programming.
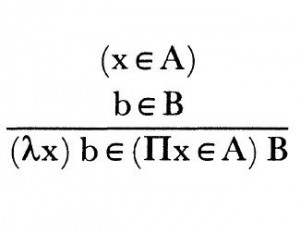
In the early 20th century, the mathematician L. E. J. Brouwer first exposed what he thought of as a scandal: mathematics, he thought, as commonly practiced, is deficient in numerical meaning. That is, we habitually take the easy route: instead of demonstrating facts concretely, we merely show that, were it not true, a logical impasse, i.e. a contradiction, would ensue. The ‘hard’ way is known as constructive mathematics. As a philosophy and methodology, constructive mathematics seems rather arcane to most practicing mathematicians. The dogma reads thus: every object contemplated needs to be constructed in a gruesome, detailed manner; and every theorem must be accompanied by the meticulous description of a process that produces witnesses of its truth. In this world, nothing happens by fiat. Yet, there is an underlying reason, beyond philosophical and methodological obstinacy, that this practice is worthwhile. Every constructive proof may be thought of as a program, or algorithm, that produces mathematical objects satisfying a certain requirement, i.e. the statement of the theorem it proves.

The relationship between constructive mathematics to computation was readily discernible. But it was not until 1971 that Per Martin-Löf formulated what logicians call a type theory for constructive mathematics: a formal language which serves the dual purpose of constructing mathematical objects, but also reasoning about them. Yet, even though logic was already gaining a following in Computer Science departments, Martin-Löf’s type theory did not gain traction until “Constructive Mathematics and Computer Programming” (CMCP) appeared in Philosophical Transactions A in 1984. The central idea of the paper is that Martin-Löf type theory can simultaneously function both as a logic for constructive mathematics and a programming language. This argument is corroborated by a translation table between common programming constructs and constructive mathematics.
A wealth of developments followed in the ensuing decades. However, a large debate remained unsettled, and that was the choice between the two versions of type theory that Martin-Löf presented: the earlier intensional theory, and the extensional theory first proposed in CMCP. The intensional theory seemed to have better logical properties, but programming in it was felt to have an unnecessarily verbose, rather Byzantine quality to it; whereas the extensional theory was easier to work with and closer to mathematical practice, but seemed to lack some strong theoretical guarantees.
Around 2005, a drastic new development swept the type theory community. A group of researchers at Carnegie Mellon University discovered a deep relationship between intensional type theory and a branch of topology, known as homotopy theory. It was then realized that the bureaucracy of intensional type theory was only thinly-veiled topological reasoning: types are spaces, programs are points, and so on. This development renewed interest in the intensional theory, and is currently paving the way towards three interrelated programmes: (a) advancing our ability to formalise and check the correctness of modern, abstract mathematics, with the assistance of computers; (b) sharpening our understanding of different notions of mathematical equality, which is fundamental to the theory of computation; and (c) deepening the exchange between pure mathematics, computation, and logic.
