To celebrate 350 years of scientific publishing, we are inviting our readers to tell us about their favourite papers from the Royal Society archive


The geometric simplicity of the flow of a fluid between differentially rotating concentric cylinders intrigued scientists long before Sir Geoffrey I. Taylor considered the problem in the Philosophical Transactions in 1923. In his 1687 Principia, Sir Isaac Newton used the flow to describe the circular motion of fluids, and in 1848 pioneering theoretician George G. Stokes considered the flow, noting the difficulty in the boundary conditions at the walls of the cylinder, now taken for granted as the no-slip boundary condition. But it was Taylor who not only made the biggest advance in understanding the flow between concentric rotating cylinders, but in the process also provided convincing evidence of the validity of the no-slip condition, proved that the Navier-Stokes equations applied to secondary flows and instabilities as well as the base flow, and provided one of the first applications of linear stability analysis that accurately predicted experimental results.
Thirty years before Taylor considered the problem, Arnulph Mallock and Maurice Couette both independently sought to measure fluid viscosity using two differentially rotating concentric cylinders, now known as a Taylor-Couette cell. Couette rotated the outer cylinder keeping the inner cylinder fixed, which is the basis for the modern viscometer. Mallock performed similar experiments, but rotated the inner cylinder keeping the outer cylinder fixed. His anomalous results (later attributed to Taylor vortices) prompted Lord Kelvin to write a letter to Lord Rayleigh in 1895 bringing the instability to his attention.
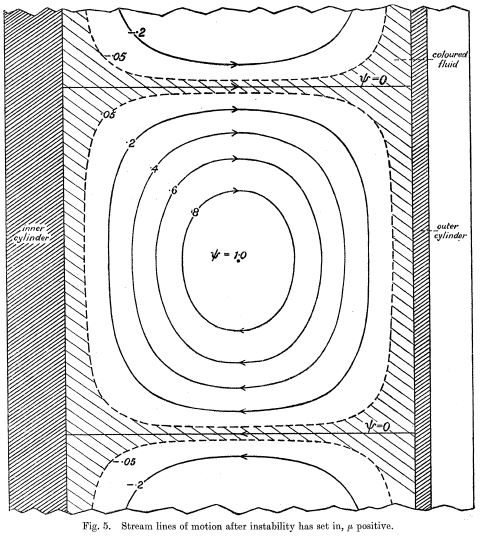
Figure from Taylor’s 1923 paper
While Rayleigh’s 1916 analysis explained the physical origin of the vortical structure as a centrifugal instability, it was not until 1923 that Taylor related theory and experiment in his Philosophical Transactions paper. Not only did he provide experimental results including photos of the instability for rotating both the inner and outer cylinders in an elegant experimental apparatus, his linear stability analysis depended on the application of the Navier-Stokes equations with no-slip boundary condition to predict the periodic vortical structures now known as Taylor vortex flow. This was a key development in the modern study of fluid mechanics, and the Taylor stability analysis is now a standard problem in many graduate fluid dynamics and stability analysis textbooks. More importantly, Taylor’s analysis provided proof of the validity of the Navier-Stokes equations with no-slip boundary conditions in the study of secondary and unstable flows. His work provided the theoretical framework for the study of bifurcation phenomena, chaotic advection, absolute and convective instabilities, and a host of other fundamental physical phenomenon and analytic methods. The paper has been referenced over 1300 times and Taylor-Couette flow along with related geophysical, astrophysical, magnetohydrodynamic, and rotating flows have been the subject of the biennial International Couette Taylor Workshop for nearly 40 years.
Tell us about your favourite paper. Click here to find out how.
