Ollerenshaw’s magic squares

Nothing is more inspiring, or more deserving of celebration, than successful research which is funded only by curiosity and rewarded only by the joy of discovery. Nothing fits this description better than Kathleen Ollerenshaw‘s work on magic squares. She first published on the subject, a total backwater of combinatorics (itself a backwater of mathematics until relatively recently), with Hermann Bondi in Philosophical Transactions A in 1982. They constructed magic squares analytically, almost for the first time since Leonhard Euler, in 1779, built them out of their much more respectable cousins, Latin squares.

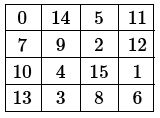
In this example, the numbers 0, …, 15 are arranged so that every row, column and diagonal sums to 30. This square does not appear explicitly in the 1982 paper (although it necessarily does, in coded form, in the appendix). Rather, it represents the object of Ollerenshaw’s subsequent heroic attack on a special class of squares, the so-called ‘most perfect’ ones. The number of general n × n magic squares is unknown, even for n = 6. Tractable subclasses are elusive. Ollerenshaw found such a class. She cracked the ‘most perfect’ problem wide open in her Proceedings A 1986 paper. She went on, with the assistance of David Brée, to give a complete enumeration for all n. She was 86 when the full account was published in 1998 as an IMA monograph, the result of nearly twenty years of work. It remains the only completely enumerated subclass of magic squares.

In an n × n most perfect square every 2 × 2 subsquare sums to 2(n² − 1) , including those which ‘wrap around’. In the 4 × 4 square above, 0 + 11 + 13 + 6 = 30 is such a wrapped sum. Additionally, on every diagonal, pairs of entries at distance n / 2 must sum to n² − 1, and this includes broken diagonals: 2 + 13 is a pair at distance 2 on the broken diagonal 14, 2, 1, 13. These two conditions are enough to force the usual ‘magic’ property: sums, columns and diagonals sum to n(n² − 1) / 2. They also force n to be a multiple of 4 (which is why the Phil Trans A paper skips to n = 8).

There are 48 most perfect squares when n = 4 (accounting for symmetry), including the one given above. When n = 8, the count jumps to 368640, and by n = 12 it is well over 22 billion. Subsequent values can be found as sequence A051235 at the wonderful Online Encyclopedia of Integer Sequences, accompanied by Ollerenshaw’s exact formula. I was stunned when I first contemplated this formula: it involves a double summation over a product over binomial coefficients of the powers in the prime factorisation of n. It is not exactly beautiful but it is unavoidable: this is a fundamental class of mathematical objects and this is how big it is. And Ollerenshaw devoted twenty years of her life to discovering this. Just because it was there.

Ollerenshaw’s life and achievements are described here at the famous MacTutor History of Mathematics Archive. The exact formula, with an explanation and examples, is described at my website.