New research published in Journal of the Royal Society Interface explores the importance of string figures in mathematics and cultural studies. Dr Roope Kaaronen from the University of Helsinki provides an overview of their work.
Can you introduce your study and explain what it is about?
You may remember playing Cat’s Cradle as a child—but did you know that making string figures is a practice found across cultures worldwide? Far from being a mere childhood folly, string figures are deeply woven into the fabric of human culture and history. They have been used as props in storytelling, religious rituals, mental puzzles, and, we argue, as tools for developing early mathematical reasoning.
Our research comprehensively documents the cultural and historical significance of string figures. An interesting feature of string figures is that they are actually so-called mathematical knots. This allows their formalisation with methods from mathematical knot theory.
By developing methods inspired by knot theory, we analysed a dataset of 826 string figures from societies across the globe. Using this dataset, we can answer a question that has intrigued anthropologists for over a century: Did similar string figures evolve independently and thus reflect cultural convergence, or do they reflect transmission from shared ancestral traditions?
Our results reveal how some string figures are remarkably globally dispersed. We interpret some of this evidence as a signal of deep shared ancestry, outlining historical migration paths and cultural connections. In other cases, patterns in string figure traditions remain unique to specific regions, suggesting possible isolation and local innovation.
How did the idea for the paper come about?
The idea for this study grew from the intersection of two research paths. Parts of our team have explored cultural practices like art and play, where string figures repeatedly appeared in ethnographic accounts. Others investigate mathematical systems embedded in material culture, such as traditional measurement systems.
The final touch was when we invited a mathematician who studies knot theory to join the team. Ultimately, we were able to blend perspectives from ethnology, archaeology, cognitive science, and mathematics. We realised how string figures could serve as a bridge between these disciplines, offering a way to explore cultural creativity with mathematical rigour. In studies on material culture, it is rare to find a cultural trait that is as amenable to formalisation and found globally. This opens new possibilities into studying how cultural traditions change and evolve over time.
What are the opportunities and challenges of interdisciplinary research in this field?
We realised how the mathematical theory of knots offers powerful tools for analysing patterns not just in string figures, but also in related practices like knotting, weaving, and ropemaking. Our work on string figures turned into a gateway for exploring the broader material culture of string-based technologies with mathematical methods. String is abundant across human societies and has been so for thousands of years but is often overlooked as a pivotal early human technology.
Challenges remain, though. Our work required countless hours of manual transcription from image to code. So, one major hurdle is automating the analysis process using computational methods. Future research will need to rely on advanced computer vision technologies to automate this process. We envision a kind of “topological fingerprinting”—much like “DNA barcoding”—which could automatically detect patterns in large samples of string technologies. Building such systems is a significant technical undertaking but one that could have dramatic implications in the study of material culture.
What are the future directions for your work?
We have already been expanding our methods to analyse other string-based practices, such as knots and fishing nets. Like string figures, these artifacts are describable using mathematical tools from knot theory. This analysis helps us to understand the evolution and shared histories of these string-based practices.
Additionally, we hope to integrate our findings with data on genetics, language, and other cultural traditions to explore how string figures fit into the broader picture of human cognitive evolution, and how these different aspects of culture coevolved with human biology or hitchhiked with particular migrations. Experimental studies could further investigate how string figures are learned and innovated, shedding light on the cognitive processes underlying their transmission. As many string figure traditions are at risk of disappearing, digitising these cultural artifacts is as timely as ever. By building computational tools to catalogue and analyse string figures, we aim to safeguard this shared human heritage for future generations.
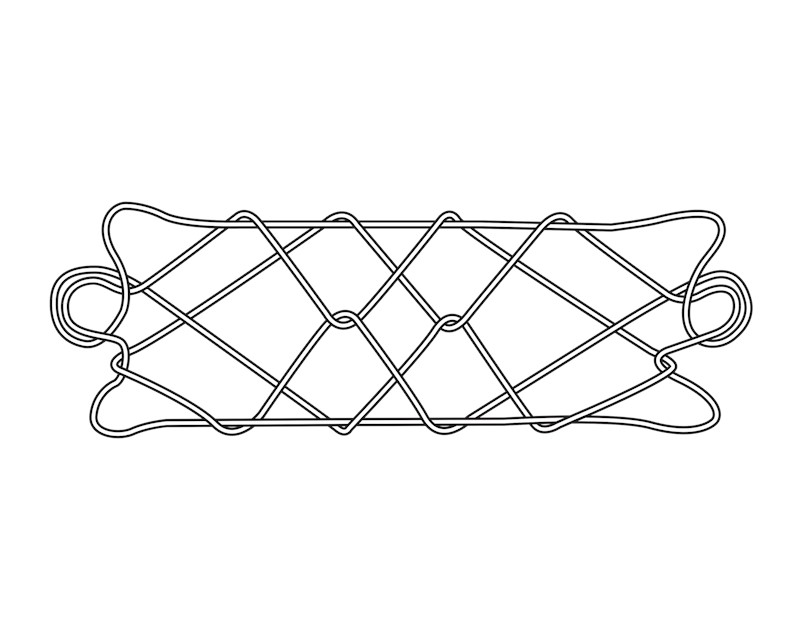
Image caption: A string figure, known by various names, made by societies throughout the Pacific region.
Keep up to date with the latest issues of Journal of the Royal Society Interface by signing up for content alerts, and browse previous issues on the journal website.




