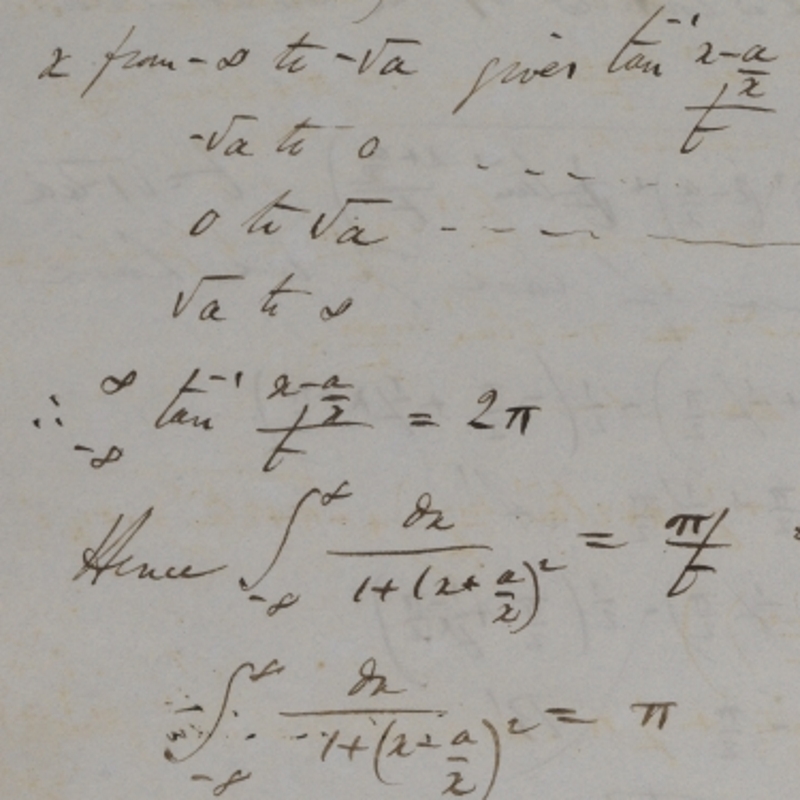Louisiane Ferlier's cataloguing of a volume of Brook Taylor correspondence at the Royal Society sheds light on the Newton-Leibniz 'calculus controversy'.
The Royal Society is inextricably linked with the priority disputes surrounding the development of calculus in the seventeenth and eighteenth centuries. As Newton versus Leibniz remains everyone’s favourite maths war, I thought it would be interesting to highlight some of its less famous participants who, it seems, managed to talk across the divide.
Brook Taylor (1685-1731) was elected to the Fellowship of the Royal Society in 1712 at the peak of the calculus controversy, before he had made the contributions to mathematics that still bear his name, Taylor’s theorem and the Taylor series. He was a Secretary of the Royal Society from January 1714 to October 1718, serving on the committee in charge of ruling on Leibniz’s claim of priority for the invention of calculus.
Portrait of Brook Taylor, ca. 1720 (RS.9685)
Many of Taylor’s manuscripts are held at St John’s College, Cambridge. Not all of them, however: his grandson, the anti-abolitionist Sir William Young, donated to the Royal Society a volume of Taylor’s correspondence, which I recently catalogued, together with the oil painting shown above. Young also published part of the correspondence, with an astonishing number of misattributions, incorrect dates and other errors. Our volume was known to historians of seventeenth-century mathematics, but its individual letters had never been catalogued in full before. Fittingly, the Brook Taylor letters are shelved in our archive strongroom alongside the Commercium Epistolicum, which includes the original correspondence collected by the Royal Society to arbitrate in the controversy between Newton and Leibniz.
Inscription in MS/82 recording the donation of the Brook Taylor correspondence
I rarely take cataloguing duties away from my archivist colleagues, but I was drawn to these letters because the mathematical correspondence is predominantly in French, my native tongue. As an aside, the letters will eventually be digitised along with correspondence of other Secretaries of the Royal Society, a project which started with the letters of Sir John Herschel. The letters from and to Brook Taylor, dated between 1712 and 1724, are fascinating, and allowed me to piece together some facts about the calculus controversies which were new to me.
Brook Taylor is usually portrayed as an ardent defender of Newton, bitterly embroiled in disputes with continental mathematicians such as Leibniz and Jean Bernoulli. His exchanges with French mathematician Pierre Rémond de Montmort, however, contradict this simple narrative and showcase the art of mathematical diplomacy. In his eulogy for Rémond written in 1719, Fontenelle described the relationship between Rémond and Taylor as ‘tender and brotherly’. Yet I must admit I wasn’t expecting Rémond to sign off his letters with ‘no one loves and honours you more than me’, ‘I kiss you with all my heart, tenderly’, and ‘I kiss you a thousand times and thousands more’!
In between declarations of love, their mathematical discussions were equally passionate: they added to each other’s work and corrected each other, but always with kindness and friendship. Rémond also shared the latest political news, discussing particularly the fallout of the 1715 Jacobite Rebellion, as well as organising a steady supply of the best French wine for Fellows of the Royal Society under the noses of French and English customs officers. Their correspondence established a solid bridge over what is usually depicted as a continental divide.
Another letter in MS/82, this time from Abate Antonio Schinella Conti to Taylor, bids to move past the calculus controversies by showing attempts to keep proceedings at the Royal Society impartial. I was surprised to read here of the role played by two women in the affair. The first, whose name Conti misspelled, is Sophia Charlotte von Kielmansegg, who – according to Conti – ordered the translation of Newton’s letter to Leibniz. She seems to have played an influential role in bringing this letter to the interest of King George I, who approved the translation. All I could find about the Countess depicts her as a courtier and mistress of the King, with no interests or patronage.
The role played by the second, Caroline of Brandenburg-Ansbach, the Princess of Wales, is better known. She corresponded with Leibniz and acted as a diplomatic go-between, writing to him: ‘What does it matter whether you or the chevalier Newton discovered the calculus?... you are the great men of our century, and both of you serve a king who merits you’. I was also taken by Princess Caroline’s description of John Flamsteed and Observatory House: ‘His house and his figure have the air of Merlin.’
Overall, the Taylor volume at the Royal Society is key for anyone interested in the development of seventeenth-century mathematics. The early letters written to John Keill, Taylor’s teacher in Cambridge, are a crucial resource enabling us to track the development of his theorem, while the extracts of Johann Bernoulli’s letters are significant primary sources in understanding the controversy surrounding Taylor’s method of increment.
The Children of John Taylor of Bifrons Park, by John Closterman, oil on canvas, 1696 (NPG 5320, via Creative Commons licence) © National Portrait Gallery, London
One element sadly missing from the volume relates to Taylor’s attempts to connect music and mathematics, which feature in his notes on the mathematical underpinnings of Jean-Philippe Rameau’s new system of music. Apart from Rémond forwarding music sheets of French airs to Taylor senior, there is little here to help us contextualise the Taylor family portrait (above), which depicts young Brook, recorder in hand, with music sheets at his feet.
I hope this has convinced you that secondary characters in the history of mathematics – and their archives – are worth investigating. After all, other forces than Newton were always at play.
