Srinivasa Ramanujan: in celebration of the centenary of his election as FRS

Event

Overview

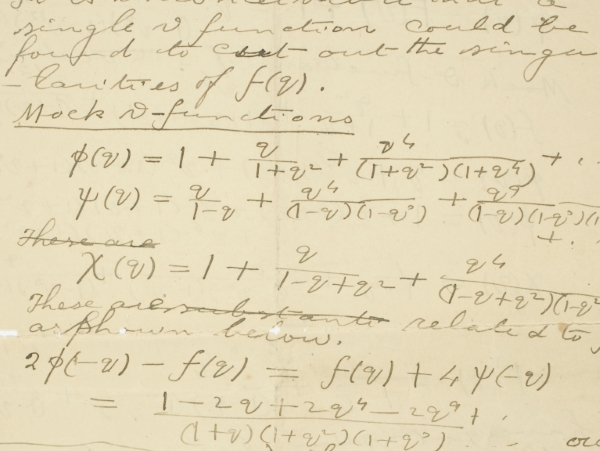
Scientific discussion meeting organised by Professor Ken Ono, Professor George E Andrews, Professor Manjul Bhargava and Professor R C Vaughan FRS.

Srinivasa Ramanujan FRS

This meeting is a celebration of the 100th anniversary of Ramanujan’s election as FRS. Distinguished scientists will speak on Ramanujan’s mathematics and its extraordinary legacy across many fields: Computer Science, Electrical Engineering, Mathematics, and Physics. The emphasis will be on recent, cutting edge research. The primary goal is to have leaders from these four important threads interact, share ideas, and develop cross-disciplinary collaborations.

The schedule of talks and speaker biographies will be available shortly. Recorded audio of the presentations will be available on this page after the meeting has taken place.

Attending this event

This meeting is intended for researchers in relevant fields.

Free to attend
Limited places, advanced registration is essential
An optional lunch can be purchased during registration

Enquiries: contact the Scientific Programmes team

Schedule of talks

15 October

Session 1 09:00-12:35

Ramanujan’s oeuvres and its mathematical legacy

9 talks Show detail

Chairs

Professor Ken Ono, Emory University, USA

Professor Ken Ono, Emory University, USA
Professor Ken Ono, Emory University, USA
- Membership status unknown
- No primary institution

Ono is the Asa Griggs Candler Professor of Mathematics at Emory University and Vice President of the American Mathematical Society. His contributions include several monographs and more than 160 research and popular articles in number theory, combinatorics and algebra. He earned his Ph.D. from UCLA and has received many awards for his research, including a Guggenheim Fellowship, a Packard Fellowship and a Sloan Research Fellowship. He was awarded a Presidential Early Career Award for Science and Engineering (PECASE) by Bill Clinton in 2000 and was named a Distinguished Teaching Scholar by the National Science Foundation in 2005. He is also a member of the US National Committee for Mathematics and the National Academy of Sciences. He was also an Associate Producer of the film “The Man Who Knew Infinity”, the Hollywood biopic about Srinivasa Ramanujan which starred Jeremy Irons and Dev Patel.

09:00-09:05 Welcome by the Royal Society

09:10-09:40 Ramanujan and his earlier notebooks

Professor Bruce Berndt, University of Illinois, USA

Show speakers

09:40-09:55 Discussion

09:55-10:25 Issues raised by Ramanujan's lost notebook

Professor George E Andrews, Pennsylvania State University, USA

Show speakers

10:25-10:40 Discussion

11:05-11:35 Ramanujan and quadratic forms

Professor Manjul Bhargava, Princeton University, USA

Show speakers

11:35-11:50 Discussion

11:50-12:20 Circle method

Professor Trevor Wooley, University of Bristol, UK

Show speakers

12:20-12:35 Discussion

Session 2 13:30-17:00

Influence on computer science and electrical engineering

6 talks Show detail

Chairs

Professor George E Andrews, Pennsylvania State University, USA

Professor George E Andrews, Pennsylvania State University, USA
Professor George E Andrews, Pennsylvania State University, USA
- Membership status unknown
- No primary institution

George E. Andrews was born in Salem, Oregon. He received his B.S. and M.A. degrees from Oregon State University, and his Ph.D. from the University of Pennsylvania. Andrews is Evan Pugh University Professor in Mathematics at the Pennsylvania State University. An expert on q-series, he has written and published more than 300 papers and has just completed (jointly with Bruce Berndt) the fifth and final volume explicating Ramanujan's Lost Notebook. Andrews was elected to the American Academy of Arts and Sciences in 1997, and to the National Academy of Sciences (USA) in 2003. He was awarded an honorary professorship at Nankai University in 2008. In 2009 he became a SIAM Fellow. He holds honorary degrees from Parma, Florida, Waterloo, Illinois and SASTRA University (India). Andrews served as President of the American Mathematical Society from February 1, 2009 to January 31, 2011, and became a Fellow of the AMS in 2012

13:30-14:00 Srinivasa Ramanujan and signal-processing problems

Professor P P Vaidyanathan, California Institute of Technology, USA

Show speakers

14:00-14:15 Discussion

14:15-14:45 From Ramanujan graphs to Ramanujan complexes

Professor Alex Lubotzky, Hebrew University, Israel

Show speakers

15:30-16:00 Sphere packing

Professor Maryna Viazovska, Ecole Polytechnique Federale de Lausanne, France

Show speakers

16:00-16:15 Discussion

16:15-16:45 The Ramanujan conjecture and its applications

Professor Winnie Li, Pennsylvania State University, USA

Show speakers

16 October

Session3 09:00-12:30

Ramanujan and number theory

8 talks Show detail

Chairs

Professor Manjul Bhargava, Princeton University, USA

09:00-09:30 Ramanujan-Petersson conjectures

Professor Peter Sarnak, Princeton University, USA

Show speakers

09:30-09:45 Discussion

09:45-10:15 Selmer groups for elliptic curves

Professor Sujatha Ramdorai, University of British Columbia, Canada

Show speakers

10:15-10:30 Discussion

11:00-11:30 Ramanujan and galois representations

11:30-11:45 Discussion

11:45-12:15 Ramanujan and the anatomy of integers

Professor K Soundararajan, Stanford University, USA

Show speakers

12:15-12:30 Discussion

Session 4 13:30-17:00

Ramanujan and physics

6 talks Show detail

Chairs

Professor Robert C Vaughan FRS, Pennsylvania State University, USA

Professor Robert C Vaughan FRS, Pennsylvania State University, USA
Professor Robert C Vaughan FRS, Pennsylvania State University, USA
- Membership status unknown
- No primary institution

Robert Vaughan has made a number of seminal contributions to the additive theory of numbers, including his demonstration of the asymptotic formula for the eight cubes problem, the proof of which had eluded many eminent predecessors. He discovered an important identity — now known as Vaughan’s identity — that has been very influential in recent number theory, and which played a substantial role in the recent elucidation of the Kummer conjecture by David Heath-Brown and Samuel Patterson. Robert is also well known for his fundamental work in multiplicative number theory done either alone or in collaboration with Hugh Montgomery, including a recent proof of a long-standing conjecture due to Erdos concerning the distribution of numbers relatively prime to a given large number, n. He was awarded the Junior Berwick Prize of the London Mathematical Society in 1979

13:30-14:00 Ramanujan's influence on string theory, black holes and moonshine

Professor Jeff Harvey, University of Chicago, USA

Show speakers

14:00-14:15 Discussion

14:15-14:45 Ramanujan and recent work on the Riemann hypothesis

Professor Ken Ono, Emory University, USA

Show speakers

14:45-15:00 Discussion

15:30-16:00 Mock modular forms are everywhere

Professor Miranda Cheng, University of Amsterdam, Netherlands

Show speakers

Srinivasa Ramanujan: in celebration of the centenary of his election as FRS

Event

October 152018

October 162018

Location

Register for this event

Overview

Attending this event

Event organisers

Professor Ken Ono, Emory University, USA

Professor George E Andrews, Pennsylvania State University, USA

Professor Manjul Bhargava, Princeton University, USA

Professor Robert C Vaughan FRS, Pennsylvania State University, USA

Schedule of talks

15 October

Session 1 09:00-12:35

Chairs

Professor Ken Ono, Emory University, USA

09:00-09:05 Welcome by the Royal Society

09:10-09:40 Ramanujan and his earlier notebooks

Professor Bruce Berndt, University of Illinois, USA

09:40-09:55 Discussion

09:55-10:25 Issues raised by Ramanujan's lost notebook

Professor George E Andrews, Pennsylvania State University, USA

10:25-10:40 Discussion

11:05-11:35 Ramanujan and quadratic forms

Professor Manjul Bhargava, Princeton University, USA

11:35-11:50 Discussion

11:50-12:20 Circle method

Professor Trevor Wooley, University of Bristol, UK

12:20-12:35 Discussion

Session 2 13:30-17:00

Chairs

Professor George E Andrews, Pennsylvania State University, USA

13:30-14:00 Srinivasa Ramanujan and signal-processing problems

Professor P P Vaidyanathan, California Institute of Technology, USA

14:00-14:15 Discussion

14:15-14:45 From Ramanujan graphs to Ramanujan complexes

Professor Alex Lubotzky, Hebrew University, Israel

15:30-16:00 Sphere packing

Professor Maryna Viazovska, Ecole Polytechnique Federale de Lausanne, France

16:00-16:15 Discussion

16:15-16:45 The Ramanujan conjecture and its applications

Professor Winnie Li, Pennsylvania State University, USA

16 October

Session3 09:00-12:30

Chairs

Professor Manjul Bhargava, Princeton University, USA

09:00-09:30 Ramanujan-Petersson conjectures

Professor Peter Sarnak, Princeton University, USA

09:30-09:45 Discussion

09:45-10:15 Selmer groups for elliptic curves

Professor Sujatha Ramdorai, University of British Columbia, Canada

10:15-10:30 Discussion

11:00-11:30 Ramanujan and galois representations

11:30-11:45 Discussion

11:45-12:15 Ramanujan and the anatomy of integers

Professor K Soundararajan, Stanford University, USA

12:15-12:30 Discussion

Session 4 13:30-17:00

Chairs

Professor Robert C Vaughan FRS, Pennsylvania State University, USA

13:30-14:00 Ramanujan's influence on string theory, black holes and moonshine

Professor Jeff Harvey, University of Chicago, USA

14:00-14:15 Discussion

14:15-14:45 Ramanujan and recent work on the Riemann hypothesis

Professor Ken Ono, Emory University, USA

14:45-15:00 Discussion

15:30-16:00 Mock modular forms are everywhere

Professor Miranda Cheng, University of Amsterdam, Netherlands

16:00-16:15 Discussion

Register for this event

October
152018

October
162018