A Modern View on Turing’s Theory of Pattern Formation

Nearly seventy years ago Alan Turing, a pioneer of Computer Science, developed a theory to explain how certain patterns in nature could arise spontaneously from simple chemical systems. This idea was a significant departure from much of his previous work on the theory of computation, and used very different kinds of mathematics. Despite the differences from his work in Computer Science, he had a similar aim of understanding something fundamental — namely, how symmetrical patterns can arise spontaneously. Among other things, Turing was fascinated by the arrangement of certain structures in plants, such as their leaves, that exhibited remarkable symmetry, even occurring in patterns of Fibonacci numbers or so-called ‘Fibonacci Phyllotaxis.’ Turing’s paper was published in Philosophical Transactions B in 1952. This was a landmark publication, opening up new vistas of scientific and mathematical exploration. 

Several aspects of this theory are striking and defy our intuition. Turing considered a chemical system which was in a stable equilibrium state, so that no net reactions were occurring, but that could be destabilised by considering the diffusion of these chemicals. In almost all other contexts we expect diffusion to lead to uniformity. Picture the spreading of a coloured dye in water for example. Turing showed that with two or more interacting chemical species, diffusion could instead induce the spontaneous creation of spatial patterns. Partly due to these unintuitive aspects of the theory, Turing's ideas were largely neglected by the biological community, which instead became fixated by the discovery of the double-helix structure of DNA a year later, and the subsequent development of molecular biology. In the 1970s, Alfred Gierer and Hans Meinhardt reintroduced the ideas of a diffusion-driven instability leading to pattern formation in their study of Hydra, a freshwater invertebrate. Since then, there has been renewed interest in these ideas, and more generally in trying to explain the underlying mechanisms of spatial organisation in developmental biology. The last thirty years especially have seen an explosion of interest in understanding pattern formation in nature in general, and the application of Turing’s theory to chemical and biological systems in particular.

This theme issue of Philosophical Transactions A reviews some of what has happened in the scientific and mathematical study of pattern formation in the decades since the publication of Turing’s paper, and looks towards the future of what challenges we have yet to overcome.

In addition to enormous advances in experimental biology, computers have radically changed how scientists analyse data and models of biological pattern formation. Below is an example of “Figure 2” from the 1952 paper, where after a painstaking effort in computing solutions of his model, Turing presents a sketch of a dappled pattern this model produces.

In contrast, we can now compute solutions of much more complicated models to a high degree of accuracy in minutes, such as the dappled pattern on the surface of a cow shown below. There are even online tools that can simulate reaction-diffusion equations in a standard web browser, such as this one, allowing anyone to explore the rich behaviours of these simple models. 

However, despite these powerful computational tools, and enormous advances in genetics and molecular biology, we still do not have a clear picture of the underlying mechanisms behind a large variety of the patterns observed in nature.

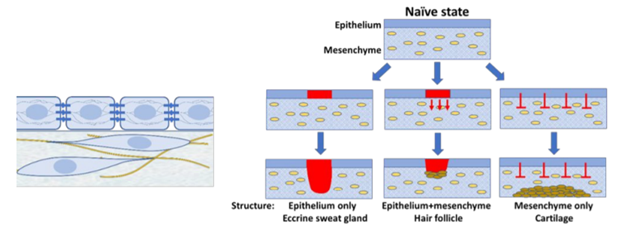
While increasing data and computational capabilities have led to an explosion of research in applying Turing’s ideas to a range of biological patterning scenarios, there are still important uncertainties in the roles played by simple reaction-diffusion processes in real biology. The third image below (taken from the paper by K. J. Painter et al) is a caricature of just a few of the kinds of structures that can occur in developing skin, where cells and extracellular structures interact both mechanically and biochemically to eventually lead to the formation of sweat glands, hair, and other structures. Turing’s original model, and many subsequent papers, have only explored the case of two interacting morphogens, but we now know that developmental processes involve hundreds of distinct chemical compounds interacting across a complex and heterogeneous environment. Still, the basic intuitions following from the idea of diffusion-driven pattern formation are powerful, and have been demonstrated in simple chemical systems, so it seems likely they play some role in a range of developmental scenarios. Despite so little of the real complexity of cellular morphogenesis being known at the time, Turing was prescient in understanding the simplicity of his ideas, stating: “This model will be a simplification and an idealisation, and consequently a falsification. It is to be hoped that the features retained for discussion are those of greatest importance in the present state of knowledge.”

Another modern advance predicted by Turing — though neglected in his initial model — is the study of cellular and mechanical forces in embryology. The articles by S. Kondo et al and F. Veerman et al highlight some aspects of these extensions which have been pursued following Turing’s idealised model. While cells interact with one another biochemically, and this is reasonably well-described by a reaction-diffusion system, they can also move, divide, die, and exert mechanical forces on one another and the intracellular environment. In recent decades scientists have made significant progress studying these cellular and mechanical forces, both on their own and in conjunction with classical biochemical interactions. While there is still much we do not know, it is clear that these mechanical aspects play important roles in how cells and tissues organise themselves, and that in many cases cells are not simply responding to chemical gradients, but serve as key drivers of symmetry breaking and pattern formation. 

S. Vittadello et al highlight the growing study of synthetic biological systems as playgrounds to explore basic mechanisms of biology in a controlled environment, and how ideas from Turing’s original analysis can give rise to design principles for synthetic biology. Such experiments can be thought of as a middle ground between the messy reality of embryology, and the simpler (yet still complex) experiments on exemplar chemical systems which were used to experimentally verify Turing’s theory in simple chemical systems in the early 1990s. C. Konow et al reviews these chemical experiments, and gives a convincing argument of the importance of simple chemical models of pattern formation. Both the synthetic and the chemical setting allow for the exploration of basic aspects of mathematical theories of pattern formation. These settings also help translate ideas from mathematical models into concrete physical examples which are valuable as an intermediary before thinking of applications beyond developmental biology, such as in medicine. These articles also highlight the multidisciplinarity of this field, and show how diverse viewpoints and tools are valuable in contributing to our collective understanding of patterns in nature.

Following Turing’s mathematical ideas, many of the papers in this theme issue explore developments in mathematical thinking about these simple models, and study aspects of extending them in new ways, such as by modelling complex geometry or in explicitly considering additional chemical gradients. These mathematical analyses provide important hypotheses to be tested experimentally, and unifying principles to help guide our thinking about our observations and data. All of the articles also suggest fruitful directions for further study.  We hope that this collection of articles serves as a useful starting point for interested students and researchers in mathematics, physics, chemistry and biology, to explore a range of research topics largely motivated by Turing’s classical paper, but where it is clear there is much left to do. 

To read more content from Philosophical Transactions A, or to find out how you can become a Guest Editor for the journal, please visit our website.

---------------------------------------------------------------

Figure captions:

Figure 1: One of the Figures from Turing’s 1952 paper, The Chemical Basis of Morphogenesis. 

Figure 2: A reaction-diffusion simulation on the surface of a cow.

Figure 3: An image from K. J. Painter et al caricaturing some of the different kinds of structures which can develop on the surface of mammalian skin, and some of the complexity of different cell types across the skin.