A new exhibition shows how mathematics was central to the work of the artist, writer and critic John Ruskin, as curator Professor Sandra Kemp explains.
A new exhibition at Brantwood, former home of artist, writer and social thinker John Ruskin (1819-1900), draws on the cultural history of mathematics to explore scientific ideas about the relationship of things and their properties to each other. Entitled ‘Ruskin’s Perspectives: The Art of Abstraction’, it shows how the geometric imagination was central to Ruskin’s work.
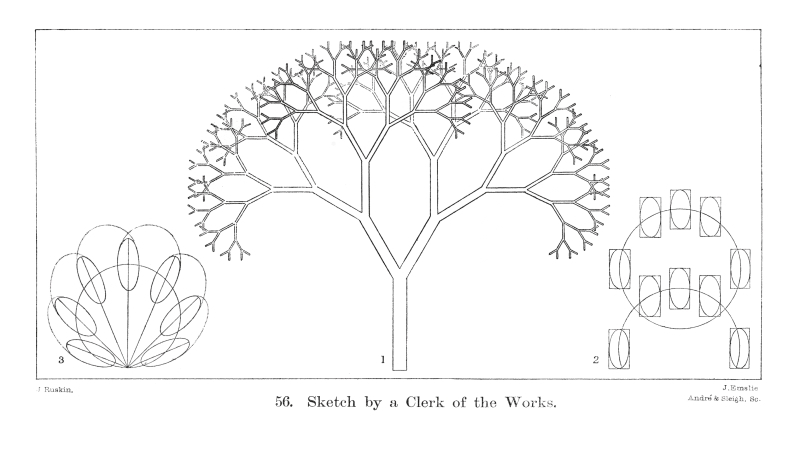John Ruskin, ‘Sketch by a Clerk of the Works’, Plate 56, Modern Painters V (London: George Allen, 1905)
The exhibition, which I’ve curated, features books on loan from the collections of the Royal Society, from coloured and embossed versions of Euclid’s Elements – the first work to argue mathematical proof through the laws of logic – to illustrated manuals on architecture by Antonio Palladio. These, alongside works from The Ruskin and Brantwood collections, illustrate not only the centrality of maths to Ruskin’s thought, but the ways in which the science of mathematics led to a new form of making art based on geometry.
Oliver Byrne (ed.), The first six books of the elements of Euclid (London: William Pickering, 1847) RCN 38538 © The Royal Society
Fascinated by form, pattern, proportion and symmetry in the world around us, Ruskin believed that mathematical knowledge underpinned both the technical proficiency and the ‘analytic power’ needed to compose a work of art. He argued that artists should acquire a working knowledge of geometry in order to understand the rules of classic linear perspective: parallel lines, the line of the horizon and the vanishing point. To this end, Ruskin produced three drawing manuals: The elements of drawing (1857), The elements of perspective (1859) – which was to be read alongside the first three books of Euclid’s Elements – and The laws of FeÌsole (1877–8). Ruskin had several editions of Euclid in his own library, alongside books on practical geometry, differential equations and algebra.
Ruskin also made frequent reference in his own works to Albrecht Dürer (1471–1528), the author of the first introductory manual of geometric theory in Europe. Writing in 1875, he noted that his illustrations for Love's Meinie involved 'a care in plume drawing which I learned in many a day's work from Albert Dürer'. Like Dürer, Ruskin combined the practical mathematics of the mason with knowledge of geometry.
Albrecht Dürer, Underweysung der Messung... (1525). RCN 2114 © The Royal Society
The exhibition shows how, in addition to the popularity of textbooks and manuals of logic aimed at the general public, recreational mathematics in the form of games was a widespread diversion in Ruskin’s time. One example, on loan from the Royal Society, is ‘Arithmetical Improvement for Children and Amusement for Young and Old Gentlemen in England’, a mathematical game originally created by brewer and amateur mathematician Henry Goodwyn (1740–1824). In challenging players to create a specific set of ‘vulgar fractions’, it touched on contemporary debate about first, the conversion of fractions to decimals (and vice versa) and second, the ordering of ‘vulgar fractions’ according to size.
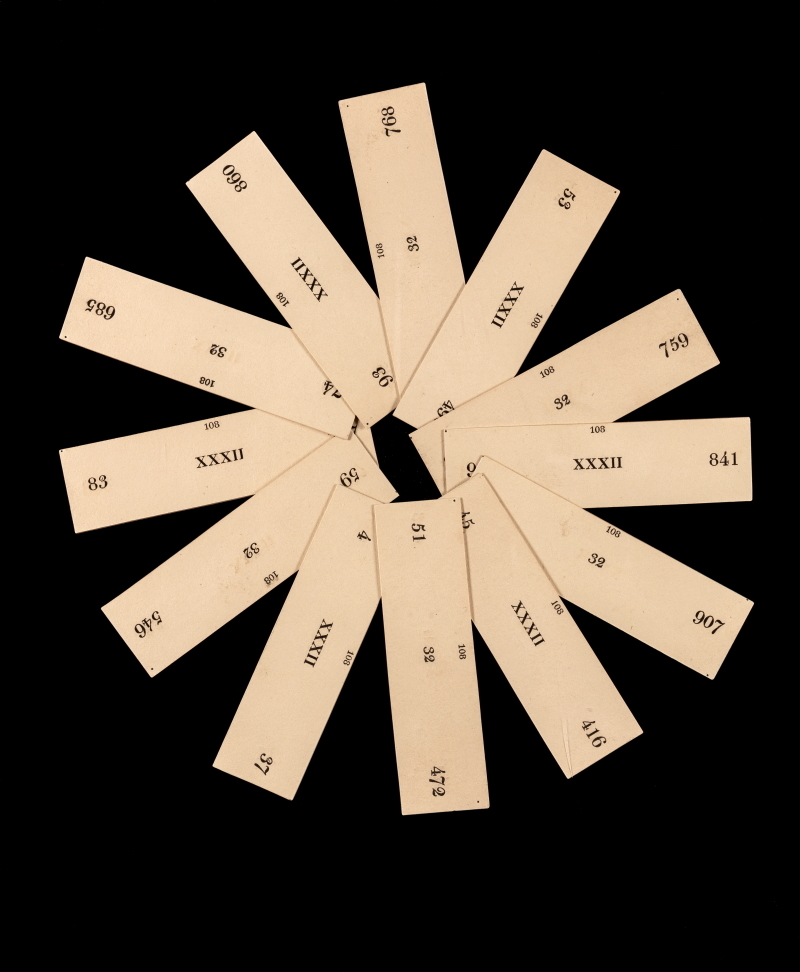Henry Goodwyn, 'Arithmetical Improvement for Children, and Amusement for Young and Old Gentlemen in England' (London: W Marchant, 1820) MS/781 © The Royal Society
Ruskin’s Perspectives explores mathematics through the lens of Ruskin’s first love: geology and mineralogy. His earliest geological interest was in glaciers, and he made studies of the diffusion of light through ice crystals in the upper atmosphere, evidence which he invoked to argue for human agency in atmospheric pollution. Ruskin was also one of the most significant mineral collectors of his time, and his personal collection amounted to more than 2500 specimens, more than 2000 of which remain at Brantwood.
The scientific study of minerals, intimately connected with plane and solid geometry, essentially began in 1812 when William Hyde Wollaston FRS (1766–1828) discovered the mathematical law of cleavage: the tendency of crystalline materials to split into fragments with identical faces. Ruskin’s collection reveals a fascination with the interplay of different chemical or environmental factors causing one crystallising process to impact upon another. He had many of his specimens cut into sections so that he could study their structure more carefully.
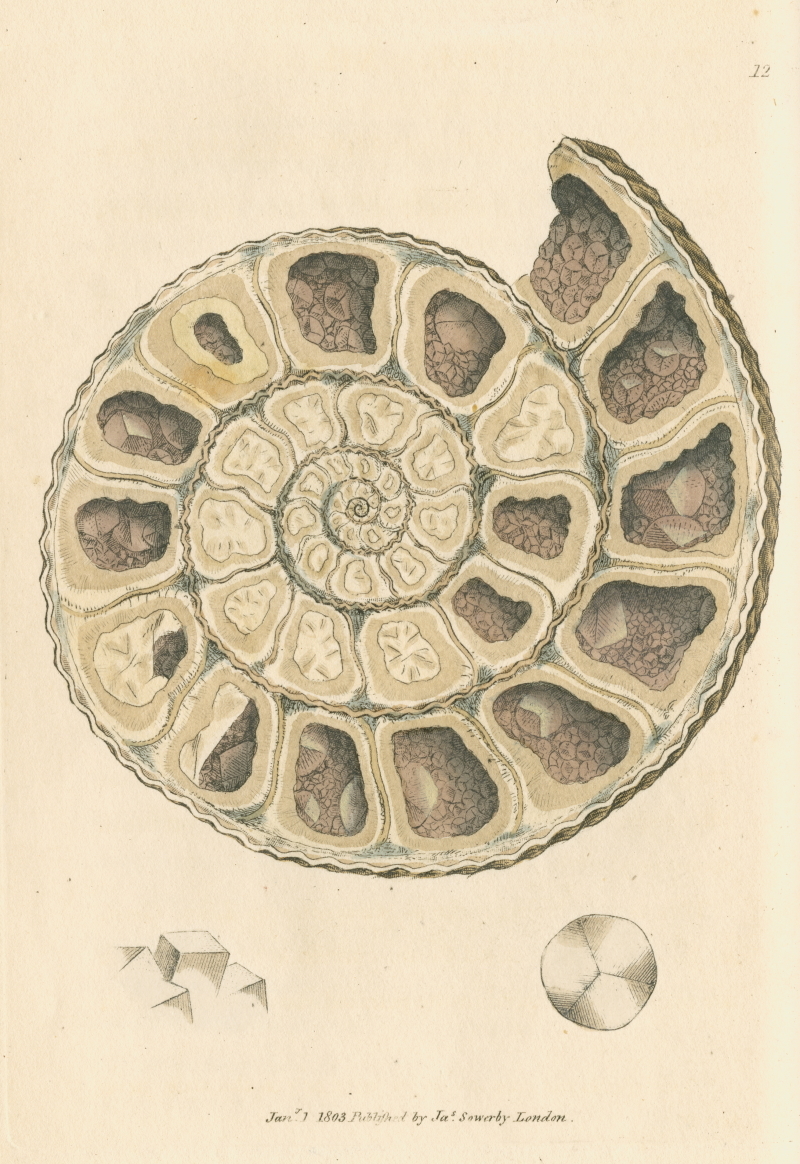James Sowerby, ‘Calx carbonata’ (Ammonite with crystals). Plate 12 from British mineralogy, vol. 1 (1803). RCN R64216 © The Royal Society
Also on loan from the Royal Society is the first volume of British mineralogy, or, Coloured figures intended to elucidate the mineralogy of Great Britain (1804) by James Sowerby (1757–1822). The illustration above, ‘Calx carbonata’ (Ammonite with Crystals), suggests logarithmic spirals, which can be interpreted using Fibonacci’s sequence – another example of the diffusion of mathematical ideas, methods, and materials through culture and into other branches of science.
From trade and travel, to the economy and decision-making based on statistics and probability, the socio-economic impact of mathematics on culture and society in Ruskin’s time was huge. Its contribution to a much broader pattern of intellectual, cultural and material history and of individuals, networks and institutions is not yet fully explored, but as our exhibition shows, the mathematical imagination was clearly central to Ruskin’s works. ‘Try always,’ Ruskin urged his students in The elements of drawing, ‘whenever you look at a form, to see the lines in it which have had power over its past fate and will have power over its futurity.’
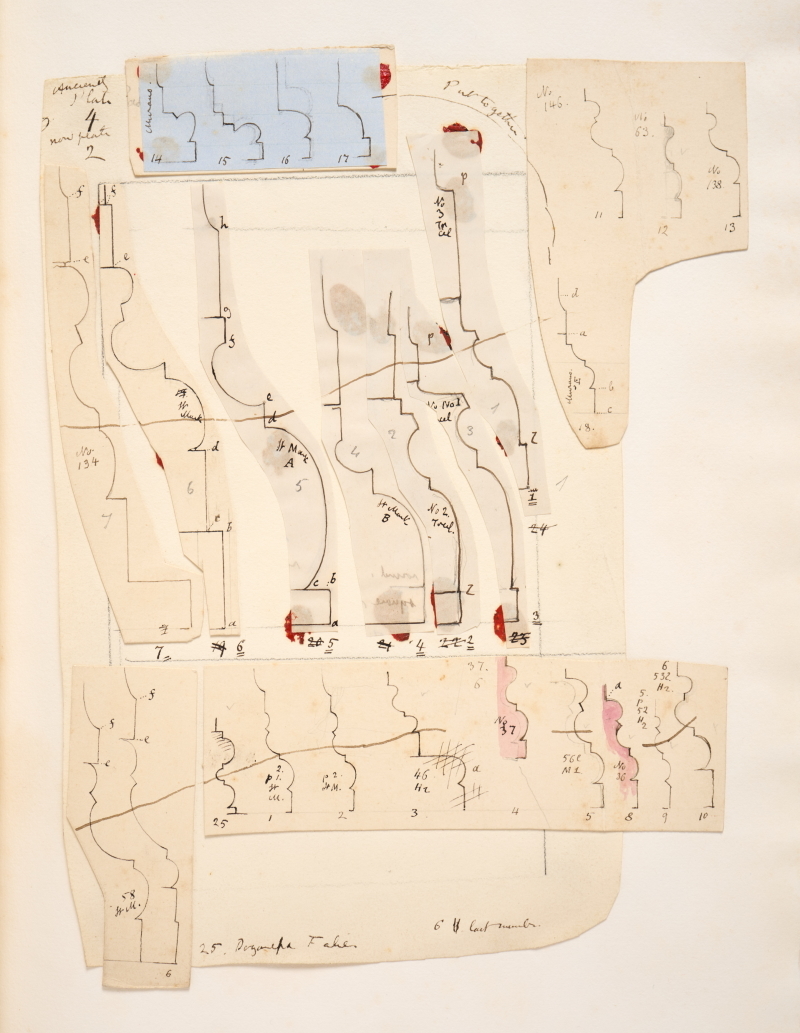John Ruskin, Venice & Verona - Album of Notes & Sketches, n.d. 1996P1642 © The Ruskin, Lancaster University
Top image: John Ruskin, Nautilus, n.d. Glass negative © The Ruskin, Lancaster University
